Highly-Eliptical-Path Ritzian Variable Star Animations Installed on 12 Jun 2007. Latest update 13 Oct 2015. Additions or changes are in bold. This page shows viewed-from-above animated examples of Willem de Sitter's (1913) binary star argument against Ritz's (1908) ballistic speed of light Electrodynamic theory. For further background information, see A Ritzian Interpretation of Variable Stars. Actual versus Apparent Binary Star Positions V(perihelion)=0.6c - Major axis diameter=1.0 Light Second (LS) Observer's distances to the right of Star A's perihelion are given in LS. Binary Orbit period = 81 seconds. No extinction. Privileged views The sequence for these three animations is linear with respect to source (grey dots) emission events. This mode of presentation doesn't provide an intuitive picture for how the apparent arrival-time bin accumulate extra hits near Star A's perihelion, but it does demonstrate the the order in which the bins get incrementally filled.

Obs. Dist: 5 LS Observed Frequencies The (A) light curve is similar to that in Figure 4 of the Ritzian Variable Stars article.

Obs. Dist: 10 LS Observed Frequencies The (A) light curve is similar to that in Figure 6 of the Ritzian Variable Stars article.

Obs. Dist: 20 LS Observed Frequencies The (A) light curve is similar to that in Figure 8 of the Ritzian Variable Stars article.

The time base for these three animations is linear with respect to apparent image arrival times. Near perihelion, some of star A's apparent images arrive from multiple locations simultaneously. As the distance between the binary and the observer increases, this effect becomes more pronounced. If a telescope's seeing cannot resolve the binary components as they move around in their orbits, then the simultaneous apparent image arrival times will appear as brightness increases. In the animations below, variable diameter dots on the left sides of the upper histograms show absolute brightness variations for star (A). (The radius of the dot is equal to the coincident arrival-time bin height.)

Obs. Dist: 5 LS

Obs. Dist: 10 LS

Obs. Dist: 20 LS

The animations are run as though there is a radio beacon associated with each component of the binary. Every tenth of a second the beacons transmit their x and y coordinates (with respect to the system's center of gravity) and the time t of the transmissions. The grey dots show what observers, located as described above, could tell about each component's path history based on received x, y, and t information. The red and blue dots show what the observer could tell, based on the transmitted x and y positions, but with the time coordinate τ derived from the arrival times of the radio signals. The histograms in the center of the animations show the filling of transmission-arrival-time bins. At the completion of each run, the bin totals form crude light curves (at the specified observer distances) for the encounter events. Highly-elliptical orbits are used to approximate near-perihelion parabolic (or hyperbolic) paths for stars involved in chance encounters. 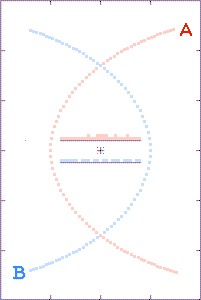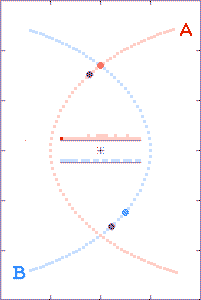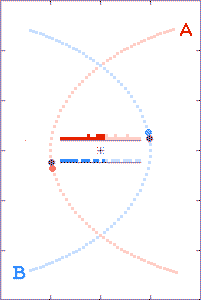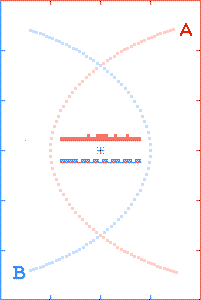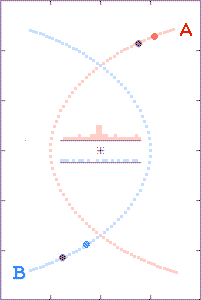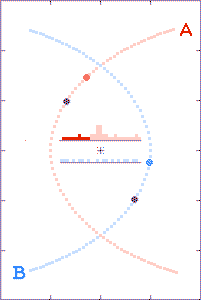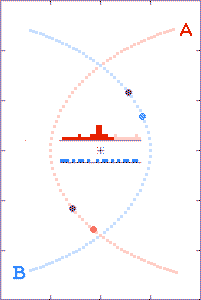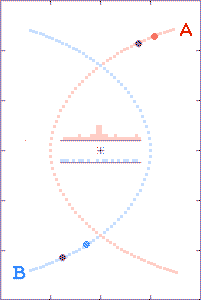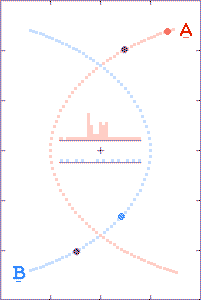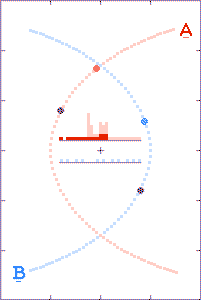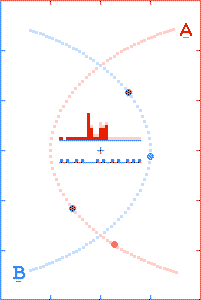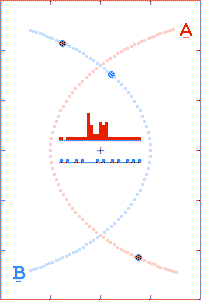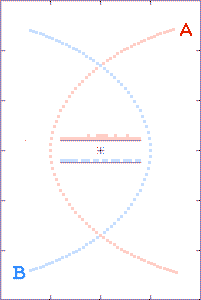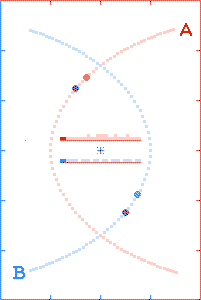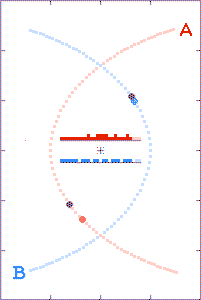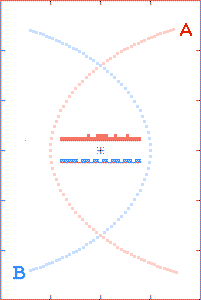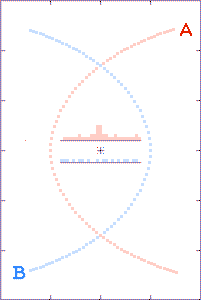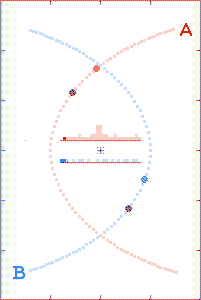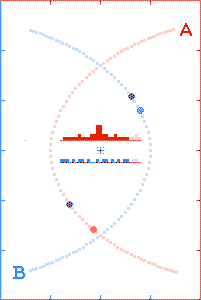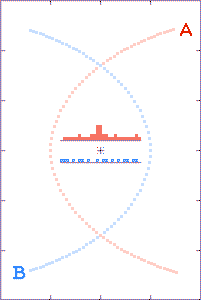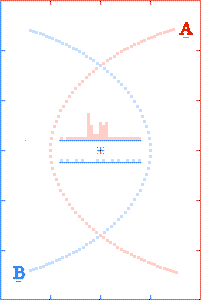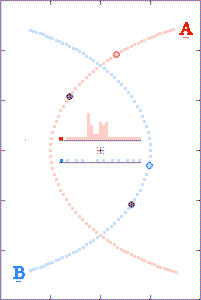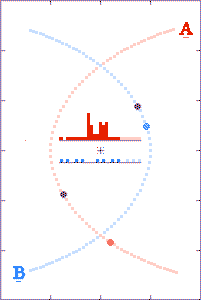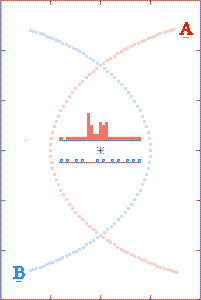In the third animation, the binary-to-observer distance is such that briefly the c+v time-advanced later emitted light arrives at the distant observer's location prior to the c-v time-retarded earlier emitted light. (In Einstein's words, the light seems to get "all mixed up.") Note the double-spiked light curve. (In the time-interval between the spikes, the starlight arriving at the observer's location even behaves as though time's arrow was reversed.) There are a lot of (yet-to-be explained) double-peaked Gamma-Ray Bursts. How it's done. Code was written in Microsoft QuickBASIC to roughly model gravitational interactions between two objects. Both objects were given the same arbitrary mass, and at t=0, object(A) was placed at x=0, y=0 and object(B) was placed at x = -1, y = 0. The program's gravitational constant, and the initial object velocities (again, with arbitrary values) were assigned and adjusted so that gravity driven parabola-like paths resulted. The incremented times, and associated x and y positions for objects(A) and (B), were transferred to columns in a Microsoft Excel spreadsheet. Position coordinates for times prior to t=0 are time-wise mirror-images of those already entered. Computational columns were then added to the spread sheet to calculate everything needed to determine the c+v arrival times at a remote location. The arrival times were assigned to discrete time bins. The number of "hits" that accumulates in each time bin serve to produce a rough light curve for the object. By using Paint Shop Pro, the real object(A) and (B) postions and their c+v apparent positions-versus-times were incorporated into graphics images (one image per time bin) and the sequence was combined to make the animation. The QuickBASIC program used to generate the binary x and y positions is: par65100.bas. The Excel files used in creating the animations (so far) are: ep65100a.xls, and ep65100q.xls. Computational Notes The the equation used in the spreadsheets to calculate light speed for binary components (A) and (B), with respect to the specially located observer, uses the vector relation C + V dot r, which is equivalent to C + V cos(θ). Here, C is the speed of light, V is the instantaneous orbital velocity for the binary component, r is the unit vector along the source-to-observer line-of-sight, and θ is the angle between the two. A more correct procedure, but harder computationally, would be to determine the required offset direction for C, compared to the line-of-sight. The offset C would then be vectorially added to V, to get the real C+V along the line-of-sight. 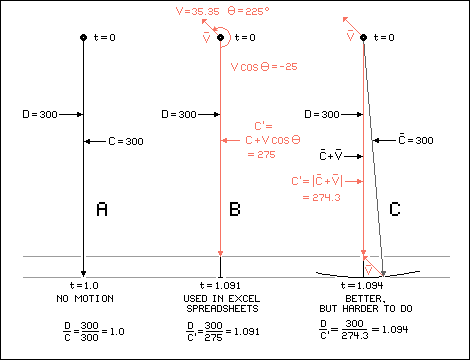The following graphs show the difference between the two ways of doing business. (Distances shown are multiples of 1 million km and speeds are multiples of 1 million km/sec.) In A, a stationary star is shown as being located 300 million km from an observer. Light, traveling at 300 million km/sec, takes one second to reach the observer. B shows the C + V cos(θ) scheme used to calculate light speeds, and hence travel times, in the spreadsheets. (This method is not vectorially correct.) In C, correct vectors for C and V are used. It can be seen that the improved C', is only slightly better (0.27 percent for this example) than the value of C' shown in B. Enroute Light Speed and Travel Time Computation Schemes Related Webpages Orbiting Binary Stars (My use of the phrase "priviledged views" above was stolen from this page.) Thanks to the visitor from (128.123.5.66) for finding a broken link to this source [09 Sep 2010].